An Introduction To Binary Heaps

In this post we are going to start a mini series on binary heaps. We will start by introducing the data structure and then talk about common algorithms in subsequent posts.

What Is A Binary Heap

A binary heap is a semi-sorted data structure that takes the form of a binary tree and has the following features:

• It is a complete binary tree, that is, all levels of the tree are filled expect maybe for the last level.
• A parent node is either greater than or equal to or less that or equal to its children.

Min Heap Vs Max Heap

A min heap is a binary heap where the parent nodes are less than or equal (\(\leq\)) to their children. A max heap is the opposite – the parent nodes are greater than or equal (\(\geq\)) to their children. Figure 1 below is an example of a min heap

Figure 1: Binary Min Heap

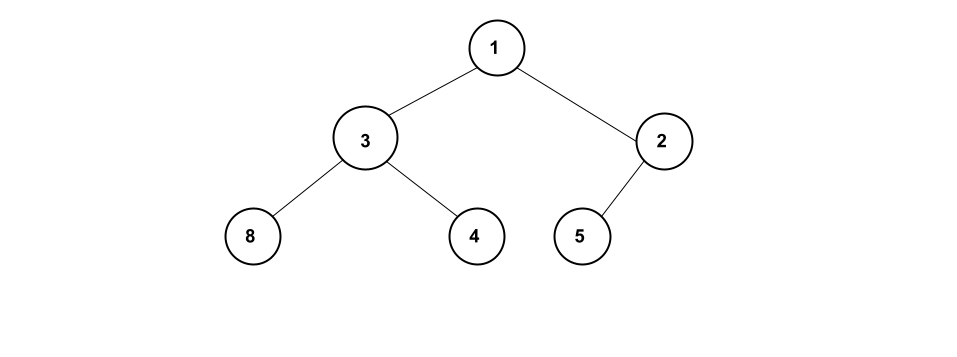
Implementation

A binary heap can be implemented using an array. All we need to know is how to find the index of a node’s parent as well as the left and right children. Here are the equations where \(i\) is the current index:

• Getting parent node’s index: \(p = \frac{(i - 1)}{2}\)

  private static int GetParentIndex(int index) => (index - 1) / 2;
  

• Getting left child index: \(l = 2 \times i + 1\)

  private static int GetLeftChildIndex(int index) => 2 * index + 1;
  

• Getting the right child index: \(r = 2 \times i + 2\)

  private static int GetRightChildIndex(int index) => 2 * index + 2;
  

We are going to implement a min heap. Let’s start by creating the class add a basic utility methods:

 public class HDMinHeap<T>
{
    private readonly List<T> _items;
    private readonly IComparer<T> _comparer;

    public HDMinHeap(IComparer<T> comparer)
    {
        _comparer = comparer;
        _items = new List<T>();
    }

    public T Root => _items[0];

    public override string ToString()
    {
        return string.Join(" ", _items);
    }

    private static int GetParentIndex(int index) => (index - 1) / 2;

    private static int GetLeftChildIndex(int index) => 2 * index + 1;

    private static int GetRightChildIndex(int index) => 2 * index + 2;

    private bool HasLeftChild(int index) => GetLeftChildIndex(index) < _items.Count;

    private void Swap(int firstIndex, int secondIndex)
    {
        var temp = _items[firstIndex];
        _items[firstIndex] = _items[secondIndex];
        _items[secondIndex] = temp;
    }
}

Inserting Item

When adding an item to a binary min heap we start by adding it to the end of the list. After than we ‘bubble up’ – comparing the item to its parent. If it’s less than its parent we swap them and repeat until the item is greater or equal to its parent. The time complexity for inserting into a binary heap is \(O(\log(n))\). Here is the code:

public void Insert(T item)
{
    _items.Add(item);
    BubbleUp();
}

private void BubbleUp()
{
    var index = _items.Count - 1;
    while (index > 0)
    {
        var parentIndex = GetParentIndex(index);
        if (_comparer.Compare(_items[index], _items[parentIndex]) < 0)
        {
            Swap(index, parentIndex);
            index = parentIndex;
        }
        else
        {
            break;
        }
    }
}

In this post we introduced a binary heap data structure and also talked about how to insert an item into a binary heap. All the code is available on GitHub. In the next post we are going to talk about popping the root of a binary heap. Till next time, thanks so much for reading.