Binary Search Tree: Introduction

Trees are data structures that consist of nodes, and each node contains a value and a list of references to child nodes. Binary trees on the other hand, are trees whose nodes have a maximum of two children. Taking it further, a binary search tree (BST) is a binary tree that has the following properties:

• All nodes of the left subtree are less than the parent node.
• All nodes of the right subtree are greater than the parent node.

Below is an image of a binary search tree. As you can see, all left subtree nodes are less than the parent node while all right subtree nodes are greater than the parent node.

Figure 1: Binary Search Tree

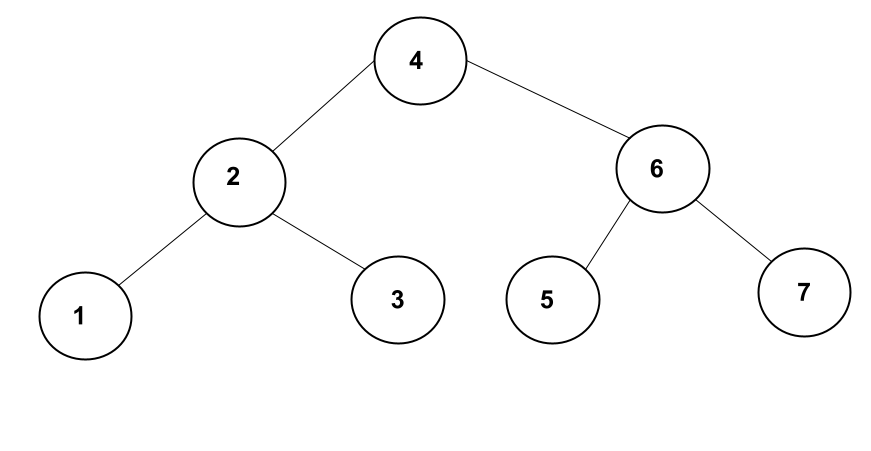
Binary search trees are very useful in situations where one needs fast lookup, addition or removal of data items. This is because the time complexity for most (all that I can think of except for traversing the tree) BST operations is \(O(\log_2(n))\) or \(O(\log(n))\) for simplicity. This is really good .

Balanced vs Unbalanced

A binary tree is said to be balanced when the height of the left subtree and the height of the right subtree of any node does not differ by more than 1. Figure 1 above is an example of a balanced tree as you can see, for all nodes, the left subtree height is the same as the right subtree height. Below is an example of an unbalanced tree.

Figure 2: Unbalance Binary Tree

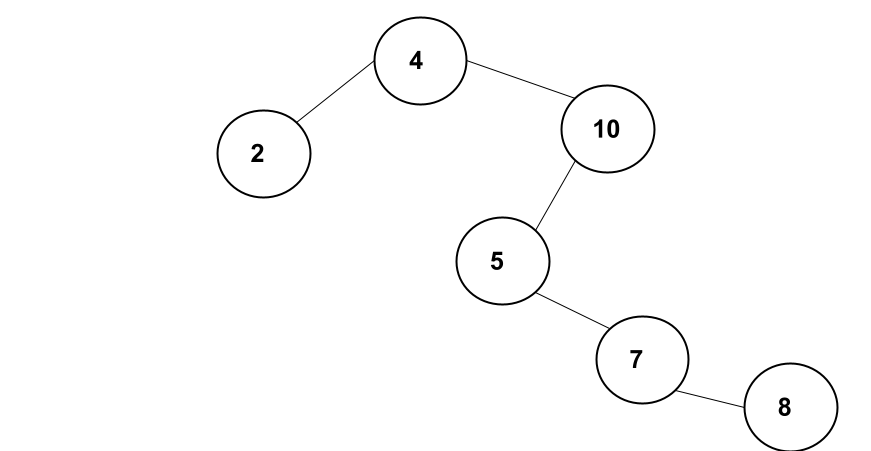
Basic Implementation

We are going to implement a basic binary search tree. Firstly, we create a the TreeNode record:

public record TreeNode<T>
{
  public T Value { get; init; }
  public TreeNode<T> Left { get; set; }
  public TreeNode<T> Right { get; set; }

  public override string ToString() => $"{Value} ";
}

Next, we create the binary search tree class:

public class HDBinarySearchTree<T> where T : IComparable
{
    private TreeNode<T> _root;
    public TreeNode<T> Root { get => _root; }
}

Inserting Items

We are going to look at how to insert an item into a binary search tree. Remember the characteristics of a binary search tree mentioned above – left subtree should be less (or equal) than the parent node and the right subtree should be greater than the parent node. Firstly, we check if the root node is null. If it is, then we instantiate it. If it exists then we go through the tree checking if the new value is greater or less than the current node’s value. If it’s less than or equal we move to the left subtree, otherwise we move to the right subtree until we reach the end (leaf node), then set the Left or Right reference of the leaf node depending on whether or not it’s value is greater or less than the new value. Time complexity of this algorithm is \(O(\log(n))\) (if the tree is as balanced as possible) while the auxiliary space complexity is \(O(1)\). Here is the code.

public void Insert(T value)
{
    TreeNode<T> newNode = new() { Value = value };

    if (_root is null)
    {
        _root = newNode;
        return;
    }

    TreeNode<T> node = _root;
    TreeNode<T> parent = null;

    while (node != null)
    {
        parent = node;
        if (value.CompareTo(node.Value) <= 0)
        {
            node = node.Left;
        }
        else
        {
                node = node.Right;
        }
    }

    if (value.CompareTo(parent.Value) <= 0)
    {
        parent.Left = newNode;
    }
    else
    {
        parent.Right = newNode;
    }
}

In this post we introduced a binary search tree data structure. We also implemented a basic binary search tree and added an algorithm to insert a new item into a binary search tree. In the next post we are going to look at how we can search for an item in a binary search tree. All the code is available on GitHub. Till next time, thanks so much for reading.