Finding A Lowest Common Ancestor In A Binary Search Tree

In the previous post we spoke about how to check if a binary tree is balance. In this post we are going to tackle a problem I encountered on LeetCode – finding the lowest common ancestor for two nodes in a binary search tree.

What Is A Lowest Common Ancestor?

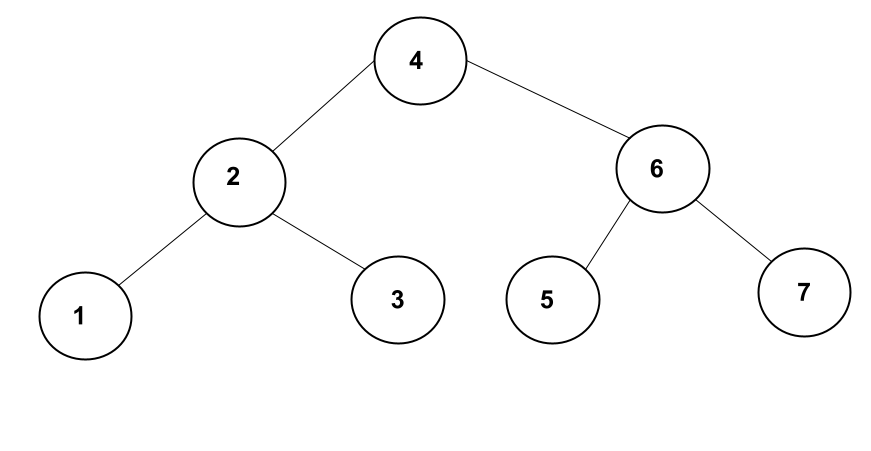
The lowest common ancestor between two nodes \(a\) and \(b\) is the lowest node in a tree that has both \(a\) and \(b\) as descendants. A node is allowed to be a descendant of itself. Using the binary search tree below the lowest common ancestor between 1 and 3 is 2. Since a node is allowed to be its own descendant, the lowest common ancestor between 6 and 7 is 6.

Figure 1: Binary Search Tree

The Code

To find the lowest common ancestor we check if the current node in the tree is greater than both nodes. If it is we move to the left. If the current node is less than both nodes we move to the right. We continue to do so until both checks are false and return the current node.

 public TreeNode<T> GetLowestCommonAncestor(T first, T second)
 {
    var node = _root;
    while(node != null)
    {
       if (node.Value.CompareTo(first) > 0 && node.Value.CompareTo(second) > 0)
       {
         node = node.Left;
       }
       else if (node.Value.CompareTo(first) < 0 && node.Value.CompareTo(second) < 0)
       {
         node = node.Right;
       }
       else
       {
         break;
       }
    }
    return node;
}

This algorithm has a time complexity of \(O(h)\) where \(h\) is the height of the tree, and space complexity of \(O(1)\). This is how one can check for the lowest common ancestor between two nodes. There is a recursive approach to this problem but it not efficient, with time complexity of \(O(h)\) and space complexity of \(O(h)\). You should always bear in mind that recursive algorithms use more space since they need to store recursive function calls on the call stack.

In this post we spoke about finding the lowest common ancestor for two nodes in a binary search tree. In the next post we are going to look at another LeetCode problem. All the code for this post is available on GitHub. Thanks for taking your time to read.