Traversing A Binary Search Tree

In the previous post we spoke about how we search for an item in a binary search tree. In this post we are going to talk about the different ways of traversing a binary search tree. There are 3 ways of traversing a binary search tree – in-order, pre-order and post-order traversal.

We are going to use the tree below for illustration:

Figure 1: Binary Search Tree

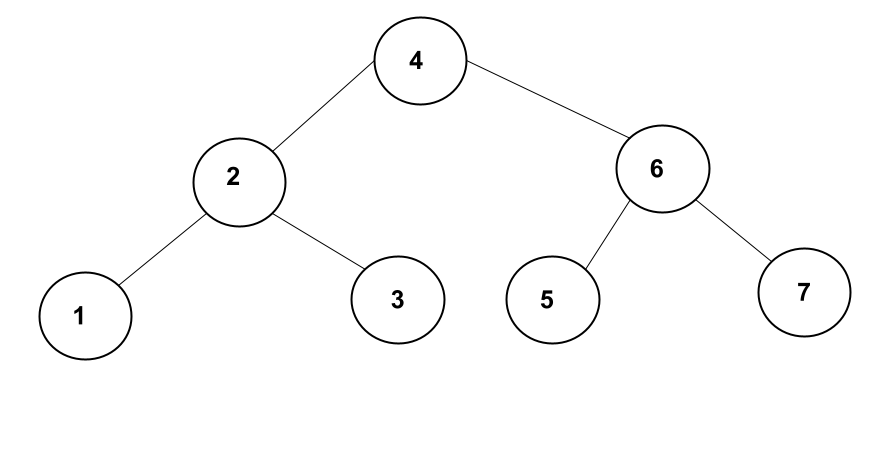
In-Order Traversal

In-order recursively moves to the left subtree, process the parent node and then moves to the right subtree. Using the tree in Figure 1 above as an example, we are going to process the nodes in this order \(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 5 \rightarrow 6 \rightarrow 7\). Here’s the code:

public void InOrderTraversal(TreeNode<T> node, StringBuilder stringBuilder)
{
    if (node is null)
    {
        return;
    }

    InOrderTraversal(node.Left, stringBuilder);

    // visit node
    stringBuilder.Append(node.ToString());

    InOrderTraversal(node.Right, stringBuilder);
}

Pre-Order Traversal

Pre-order traversal first processes the root node then recursively move to the left subtree, and lastly move to the right subtree. It creates a copy of the tree. Pre-order traversal of the tree in Figure 1 above would process the nodes in this order \(4 \rightarrow 2 \rightarrow 1 \rightarrow 3 \rightarrow 6 \rightarrow 5 \rightarrow 7\). Here’s the code:

public void PreOrderTraversal(TreeNode<T> node, StringBuilder stringBuilder)
{
     if (node is null)
    {
        return;
    }

    // visit node
    stringBuilder.Append(node.ToString());

    PreOrderTraversal(node.Left, stringBuilder);

    PreOrderTraversal(node.Right, stringBuilder);
}

Post-Order Traversal

Post-order traversal first traverses the left subtree, then the right subtree before processing the parent node. Using the tree in Figure 1, we would process the nodes in the following order: \(1 \rightarrow 3 \rightarrow 2 \rightarrow 5 \rightarrow 7 \rightarrow 6 \rightarrow 4\). Here’s the code for post-order travesal:

public void PostOrderTraversal(TreeNode<T> node, StringBuilder stringBuilder)
{
    if (node is null)
    {
        return;
    }

    PostOrderTraversal(node.Left, stringBuilder);

    PostOrderTraversal(node.Right, stringBuilder);

    // visit node
    stringBuilder.Append(node.ToString());
}

Time complexity for these algorithms is \(O(n)\) while auxiliary space complexity is also \(O(h)\), where \(h\) is the height of the tree. If the tree is balanced then \(h = \log(n)\) so the best case scenario of auxiliary space complexity is \(O(\log(n))\). A skewed tree, which is worst case scenario will have auxiliary space complexity of \(O(n)\).

In this post we spoke about how we can traverse a binary search tree using in-order, pre-order as well as post-order traversal. All code for this post is available on GitHub. Feel free to leave a comment if you have a question and/or suggestion. Thanks so much for reading.