Count The Number Of Connected Components In A Graph

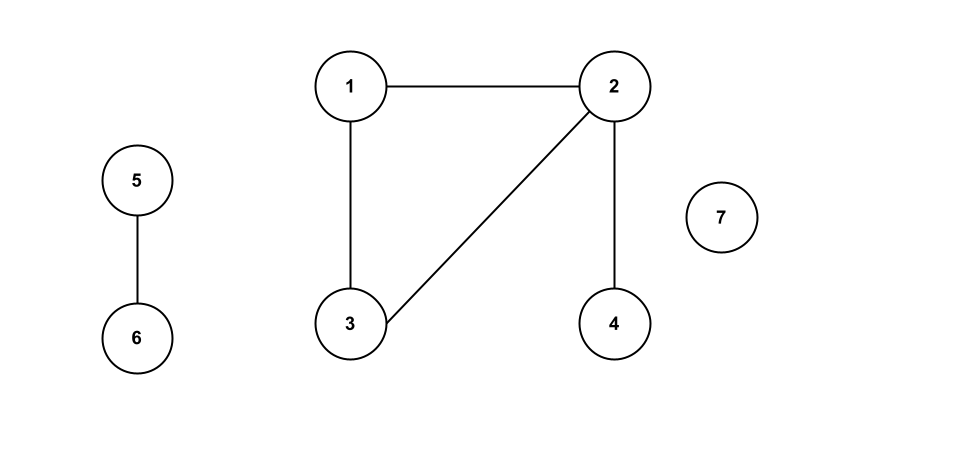
In the previous post we implemented an algorithm that finds the shortest path between two vertices in a graph. In this post we are going to solve a LeetCode problem that requires us to count the total number of connected components in a graph. Using Figure 1 below as an example, our graph has 3 connected components. All we need to do is write an algorithm that counts them.

Figure 1: Connected components

Solution

To solve this problem we are going to do a combination of iterative and recursive functions. We need to iterate through all the vertices in the graph and for each vertex, recursively run through it’s neighbors until we have visited every vertex in the connected component. We need to ensure we don’t double-count our vertices so we should maintain a set of visited components. We return false if a vertex has already been visited and true after we have successfully traversed through a connected component. When our recursive function returns true we increment the our count of connected components. Here’s the code:

public int GetTotalConnectedComponents()
{
    int count = 0;
    HashSet<T> visited = new();
    foreach(var vertex in _adjacentList.Keys)
    {
        if (Traverse(vertex, ref visited))
        {
            count++;
        }
    }
    return count;
}

private bool Traverse(T vertex, ref HashSet<T> visited)
{
    if (visited.Contains(vertex))
    {
        return false;
    }

    visited.Add(vertex);

    foreach (var neighbor in _adjacentList[vertex])
    {
        Traverse(neighbor, ref visited);
    }

    return true;
}

In this post we spoke about an algorithm that counts the number of connected components in a graph. All the code is available on GitHub. Leave a comment if you have any questions and/or suggestions. Till next time, thanks so much for taking your time to read.