Introduction To Graphs

In this post we are going to talk about the graph data structure. A graph is a data structure that consists of vertices (also known as nodes) and a set of edges that connect the vertices. It is used to represent relationships between objects such as one’s social network friends, cities in a country or build dependencies in a build pipeline. Before we jump into the code we want to look into the theory of graphs – different types of graphs and different ways to represent them.

Directed Vs Undirected Graphs

A graph can be either directed or undirected. A directed graph (also known as a digraph) is a graph in which the edges have a direction. In Figure 1 below there is an edge between 1 and 3 with a direction going towards 3. This means you can go from 1 to 3 but not the other way round. Think of it like a one-way road from 1 to 3.

Figure 1: Directed graph

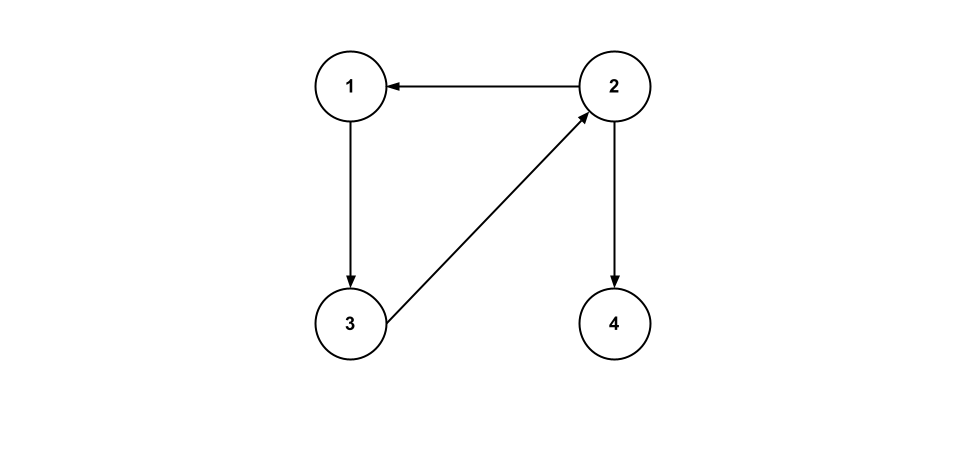
An undirected graph is a graph in which edges don’t have specific directions. You can move from one vertex to the other and vice versa. Figure 2 below is an example of an undirected graph. You can move from 1 to 3 as well as from 3 to 1.

Figure 2: Undirected graph

Weighted Vs Unweighted Graph

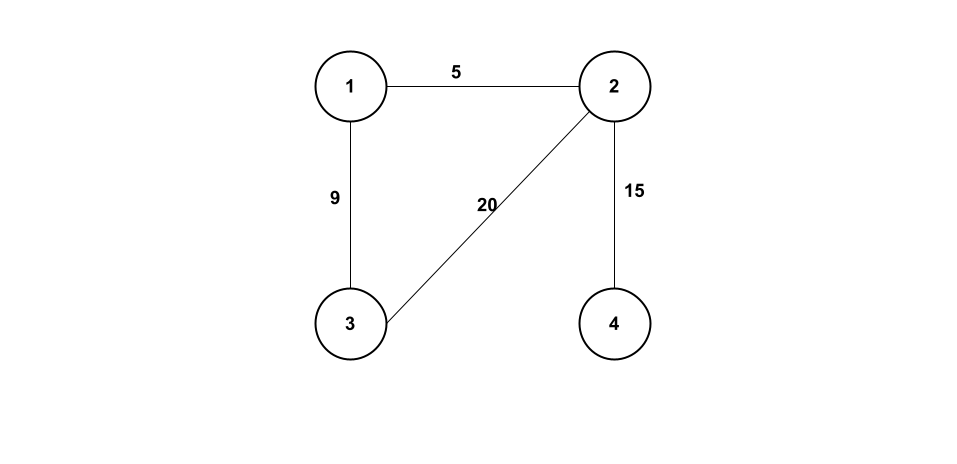
A weighted graph is a graph in which the edges have a numerical weight associated with them. Using an example of a graph representing connections between cities the weights can represent the distance between two cities. Figure 3 below is an example of a weighted graph while figures 1 and 2 above are examples of unweighted graphs.

Figure 3: Weighted graph

Representing Graphs In Code

There are two ways of representing a graph in code – adjacency matrix and adjacency list. Each one has its pros and cons.

Adjacency matrix

An adjacency matrix is a \(n \times n\) matrix where \(n\) is the number of vertices in a graph. In code we can use a two dimensional array. When there is an edge between two vertices \(i\) and \(j\) the value at \(A[ i ][ j ]\) is set to 1 (true) otherwise the value is 0 (false). Figure 4 below is an example of an adjacency matrix representing the undirected graph in Figure 2 above.

Figure 4: Adjacency matrix

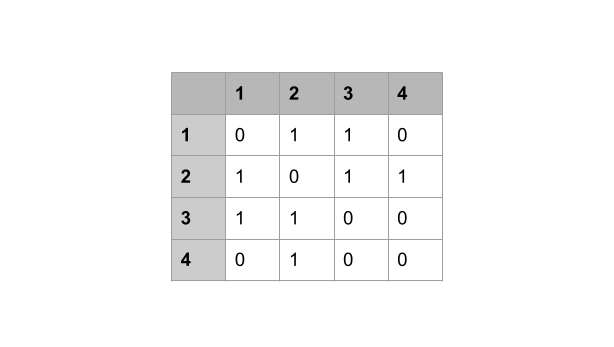
Adjacency matrices are very useful when you want to quickly check if there is a connection between two nodes. You just get the value at \(A[ i ][ j ]\) in \(O(1)\) time. We can also add or delete an edge in \(O(1)\) time. However, adjacency matrix take too much space – \(n^2\) where \(n\) is the number of vertices. If you have only one edge in that graph then you will have a lot of wasted space. Traversing an adjacency matrix requires \(O(n^2)\) time since it’s a two dimensional array. I still have nightmares from my time in school when we were using adjacency matrices in my Graph Theory class. And to make it worse, we were doing everything by hand .

Adjacency List

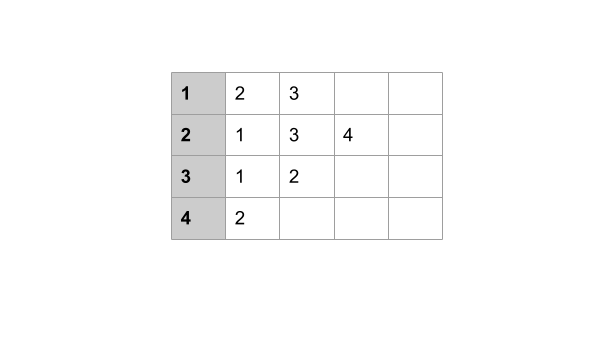
An adjacency list is a list of vertices with each vertex containing a list of vertices it’s connected to. There are multiple ways of representing this in code. I prefer using a dictionary (hash map) with the keys being the vertices and the values a set (hash set) of vertices. Something like Dictionary<T, HashSet<T>>. The reason why I like this representation is because adding or removing an edge takes only \(O(1)\) time. Also checking is there is an edge between two vertices takes \(O(1)\). Had we used an array then we would be looking at \(O(n)\) time complexity. Figure 5 below is an adjacency list representation of the graph in Figure 2 above.

Figure 5: Adjacency list

The Code

We are going to create a basic graph using an adjacency list and add one function to add a vertex. Other functions are going to be added in subsequent posts.

public class HDGraph<T>
{
    private readonly Dictionary<T, HashSet<T>> _adjacentList;

    public HDGraph()
    {
        _adjacentList = new Dictionary<T, HashSet<T>>();
    }

    public void AddVertex(T vertex)
    {
        if (!_adjacentList.ContainsKey(vertex))
        {
            _adjacentList[vertex] = new HashSet<T>();
        }
    }
}

In this post we introduced the graph data structure, explained different types of graphs as well as different ways to represent graphs in code. We also created a simple graph model and added a function to add a vertex. All the code is available on GitHub.