Traversing A Graph

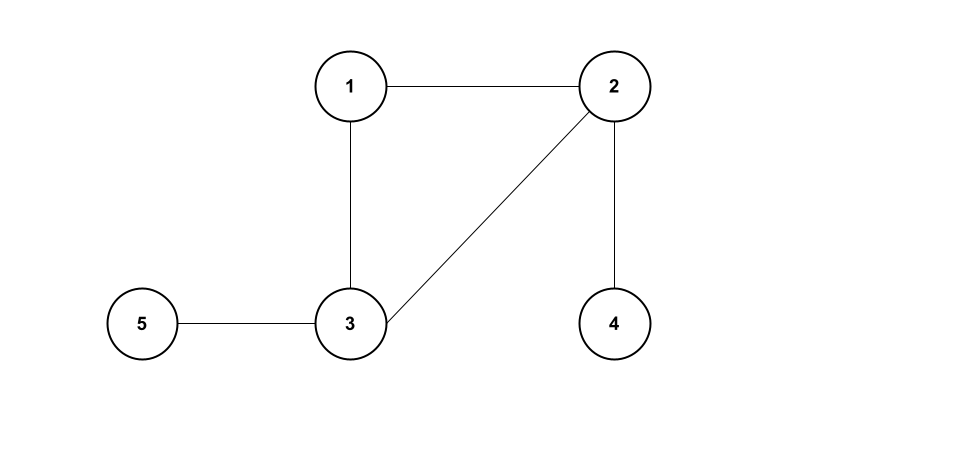
In the previous post we spoke about how we can remove an edge between two vertices in a graph. In this post we are going to talk about two different ways of traversing a graph – depth first and breadth first traversal. Below is the graph that we will use as an example when we talk about the two algorithm.

Figure 1: Undirected graph

Now let’s talk about depth first and breadth fist traversal.

Depth First Traversal

When we use depth first traversal we start at a given vertex and explore as far as possible along each brach before going to other branches. Using our graph in Figure 1 as an example, if we start at 1 we can either take the branch that goes to 2 or the one that goes to 3. Let’s say for argument’s sake we take the one that goes to 3. We will go all the way to 5 before we go to the branch that goes via 2. The order of traversal will look like this \(1 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 4\). Now let’s implement this in code.

We are going to take the iterative approach in this example. There is a recursive approach as well. To do this we are going to need a stack. We push the starting node into the stack and then when we run an iteration until the stack is empty doing the following: pop an item from the stack, if item has not been visited, visit it and mark it as visited (adding it to the visited set). Then push all of the item’s neighbors into the stack. We need to ensure we mark vertices as visited otherwise we’ll have an infinite loop. The time complexity for this algorithm is \(O(n + k)\) where \(n\) is the number of vertices and \(k\) is the number of edges in the graph. The space complexity is \(O(n)\). Here’s the code:

public string RunDepthFirstTraversal(T start)
{
    if (!_adjacentList.ContainsKey(start))
    {
        return null;
    }

    StringBuilder stringBuilder = new();
    Stack<T> stack = new();
    HashSet<T> visited = new();
    stack.Push(start);

    while(stack.Count > 0)
    {
        var current = stack.Pop();
        if (!visited.Contains(current))
        {
            visited.Add(current);
            stringBuilder.Append($"{current} ");
            foreach(var neigbor in _adjacentList[current])
            {
                stack.Push(neigbor);
            }
        }
    }

    return stringBuilder.ToString().Trim();
}

Now let’s talk about breadth first traversal.

Breadth First Traversal

With breadth first traversal we traverse the graph level by level instead of taking one branch and going through it to the end. Looking at our example graph in Figure 1, if we start at one and choose to go to 3 first, we will then have to go to 2 before going to the next level of 5 and 4. The order of traversal in this case will be \(1 \rightarrow 3 \rightarrow 2 \rightarrow 5 \rightarrow 4\).

We will implement breath first traversal iteratively just like we did with the depth first algorithm. However, instead of using a stack we use a queue. The rest is the same and both algorithms have the same time and space complexity. Here’s the code:

public string RunBreadthFirstTraversal(T start)
{
    if (!_adjacentList.ContainsKey(start))
    {
        return null;
    }

    StringBuilder stringBuilder = new();
    Queue<T> queue = new();
    HashSet<T> visited = new();
    queue.Enqueue(start);

    while (queue.Count > 0)
    {
        var current = queue.Dequeue();
        if (!visited.Contains(current))
        {
            visited.Add(current);
            stringBuilder.Append($"{current} ");
            foreach (var neigbor in _adjacentList[current])
            {
                queue.Enqueue(neigbor);
            }
        }
    }

    return stringBuilder.ToString().Trim();
}

In this post we spoke about the two algorithms used to traverse a graph. All the code used in this post is available of GitHub. In the next post we are going to talk about how we can determine if there is a path between two vertices. Till next time, thanks so much for taking your time to read.